比特币的加密算法
比特币使用了secp256k1、SHA256、RIMP160、Base58等密码学内容。secp256k1属于椭圆曲线签名算法(ECDSA);SHA-256和RIPEMD-160属于HASH摘要算法;Base58则是比特币自己定义的编码方式,去除了Base64编码中的特殊字符和容易看错的字符。椭圆曲线加密算法有好几个标准:
NIST, Recommended Elliptic Curves for Government Use
SECG, SEC 2: Recommended Elliptic Curve Domain Parameters
ECC Brainpool, ECC Brainpool Standard Curves and Curve Generation
本文主要介绍椭圆曲线签名算法secp256k1,其由上述第二个标准给出。
secp256k1⌗
secp256k1是由(Standards for Efficient Cryptography)定制的一种椭圆曲线签名算法,在比特币流行以前,该算法几乎没有被使用过。大多数常用的曲线具有一个随机的结构,但是secp256k1是为了更有效率的计算而构造了一个非随机结构。因此如果该算法的实现通过合理的优化,其计算效率可以比别的曲线快30%以上。同时,与常用的NIST曲线不同,secp256k1的常量是通过可预测的方式挑选的,这可以有效的减少防止曲线设计者安置后门的可能性。具体规范可以参考Secp256k1和SEC-V2。
椭圆曲线签名算法⌗
椭圆曲线签名算法通过Diffie–Hellman密钥交换方式来工作,其一般的数学描述如下:
给定一个阶$n$的有限群$G$。$\forall g\in G$,$\exists p\in N$,满足$g^p =e$, 其中$e$为群$G$的单位元,$p$为元素$g$的阶。选取$k\in N$,满足$0<k<p$,则$\exists h\in G$使得$h=g^k$。 当$k$为非常大的数时,已知$h,g$,逆向求解$k$将会变的很困难,此问题称之为离散对数问题(DLP)。根据拉格朗日定理,$n$必定被$p$整除,因此$n=p*r$,$r$称之为cofactor。此时$(G, g, p, r)$构成一组公钥密码体系。可以选取$k\in N$满足$0<k<p$作为私钥,$g^k$作为公钥。
根据以上定义,我们来构建密码交换流程,假设通信双方为Alice和Bob:
Alice选择一个随机自然数$a$,然后将$g^a$发送给Bob
Bob选择一个随机自然数$b$,然后将$g^b$发送给Alice
Alice计算$(g^{b} )^a$
Bob计算$(g^{a} )^b$
根据上述定义,由$g$生成的集合为一个循环群,而所有循环群均为阿贝尔群,任意两个元素乘积是可以交换的,因此有 $$(g^{b} )^{a} =g^{ab} =(g^{a} )^{b}$$ 故而Alice和Bob可以协商出共同的信息$g^{ab}$,它可以作为共享密钥。以上描述中$(a,g^a)$为Alice的私钥和公钥,$(b,g^b)$为Bob的私钥和公钥。
椭圆曲线名称的来源⌗
椭圆曲线的名称来自于对椭圆周长的积分,通过一定的技巧,总是能够得到具有$$\int_{\alpha}^{\beta} {\frac{dx}{\sqrt{x^3+ax+b}}}$$的形式的积分项,因此这种方程形式的曲线被叫做椭圆曲线。除了椭圆积分以外,椭圆曲线还和费马大定理存在紧密的联系,后者给出的等式可以通过初等变换的方式变成椭圆曲线方程。因此,费马大定理可以被转化成求解椭圆曲线。
椭圆曲线的数学描述⌗
椭圆曲线的一般方程为$y^2 +axy+by=x^3 + cx^2 +dx+e$ ,根据不同的参数条件,可以简化成不同的形式,这里只列出secp256k1使用的形式: $$y^2 =x^3 +ax+b$$ 其中$4a^3 +27b^2\ne0$。
以下给出两个椭圆曲线的例子:
a. 曲线 $y^2 =x^3 -x$
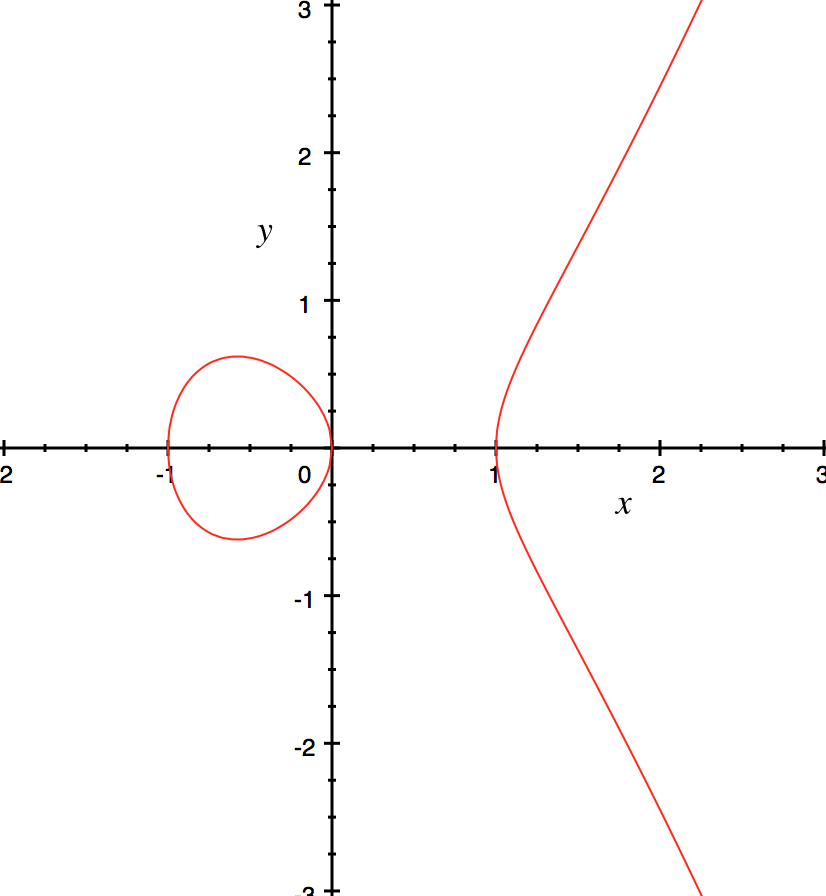
b. 曲线 $y^2 =x^3 -x +1$
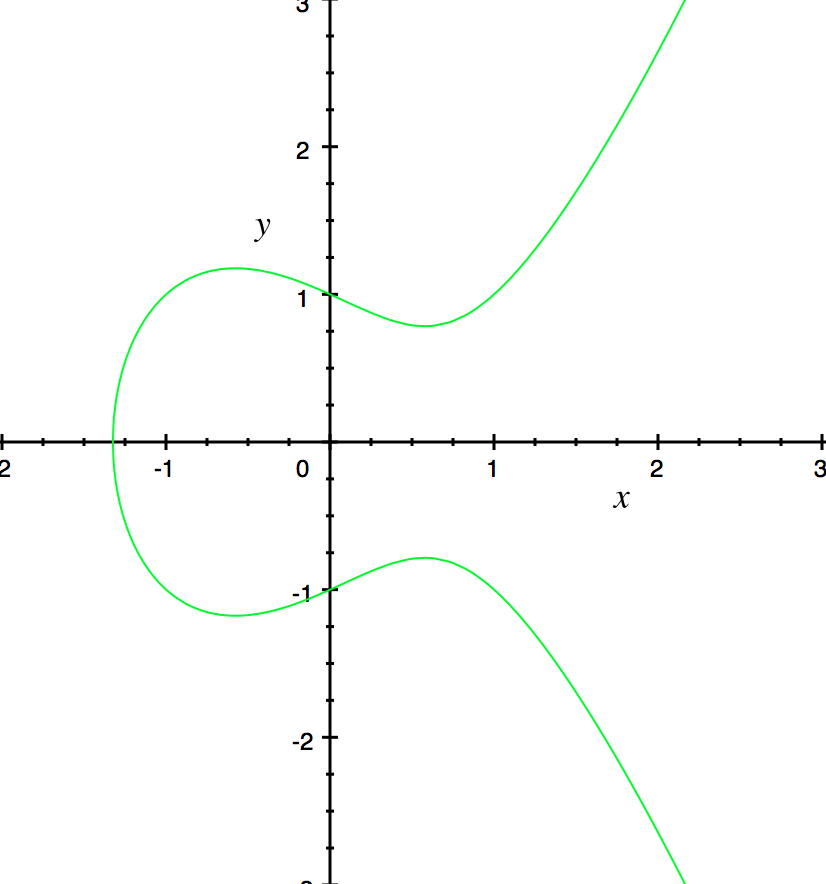
根据椭圆曲线理论,椭圆曲线$y^2 =x^3 +ax+b$在$(x,y)$平面上所有点构成的集合$E$,和该平面上的无穷远点$\mathcal{O}$可以构成一个集合$\overline{E}\equiv E\cup\mathcal{O}$,其上可以构造一组加法规则。构造$(\overline{E},+)$形成一个加法群。加法规则如下:
- 对于$\mathcal{O}$,满足 $$\mathcal{O}+\mathcal{O}=\mathcal{O}$$
- 对于椭圆曲线上任意一点$$(x,y)+ \mathcal{O} = \mathcal{O} + (x,y) = (x,y)$$
- 对于任意点$(x,y)$,存在一个逆元$(x,-y)$,使得$$(x,y)+(x,-y)=\mathcal{O}$$
- 对于任意x轴不同的两点$(x_1,y_1)$、$(x_2,y_2)$,可以构建$$(x_1,y_1)+(x_2,y_2)=(x_3,y_3)$$ 其中$x_3=\lambda^2 -x_1-x_2$,$y_3=\lambda(x_1-x_3)-y_1$,$\lambda=(y_2-y_1)/(x_2-x_1)$
- 对于任意一点$(x,y)$,可以对自身做加法,使得$$(x,y)+(x,y)=2(x,y)=(x_3+y_3)$$ 其中$x_3=\lambda^2 -2x$,$y_3=\lambda(x-x_3)-y$,$\lambda=(3x^2+a)/(2y)$
椭圆曲线加法的几何意义⌗
上述定义可以对应到实平面上的几何曲线:

蓝色、绿色和粉色直线分别表示了与椭圆曲线相交的几种不同类型的直线。
蓝色线为普通的相交线,和椭圆曲线相交于三个点$P,Q,-(P+Q)$,三者之和为$P+Q+(-(P+Q))=\mathcal{O}$
绿色线为切线,和椭圆曲线切于点$R$,交于$-2R$,切点当作两点,三者之和为$R+R+(-2R)=\mathcal{O}$
粉色线为特殊切线,和椭圆曲线切于一个点,别的点不相交,则该点$O$可以被定义为$O=\mathcal{O}$
蓝色和绿色虚线均和椭圆曲线交于两点,分别的可以得到$(P+Q)+(-(P+Q))=\mathcal{O}$和$(2R)+(-2R)=\mathcal{O}$
以上分析符合前面定义的加法规则,可以看出,与椭圆曲线相交的直线上,所有交点之和为$\mathcal{O}$。
有限域上的椭圆曲线⌗
之前讨论的椭圆曲线均是构建在实数域$\mathcal{R}$上的,通过二维平面构成连贯的线条。若要把椭圆曲线及其之上构建的加法规则应用到密码学,则需要换成有限域或伽罗瓦域。有限的意思是域上的元素个数有限,不是无穷的;域则是可以进行加减乘除四则运算的集合。
有限域$\mathcal{F}_p$的数学构造⌗
任意质数$p$,都可以构造一个整数模$p$,记作$\mathbb{Z}/n\mathbb{Z}$或$\mathcal{F}_p$,其为一个有限域,该域的序(元素总数)为$p$。
有限域$\mathcal{F}_p$上的椭圆曲线⌗
如果把椭圆曲线应用到有限域$\mathcal{F}_p$上,则椭圆曲线在$(x,y)$平面上的点变成了一组离散的点集。一个例子如下:
曲线 $y^2 =x^3 +2x+3 \bmod{5}$
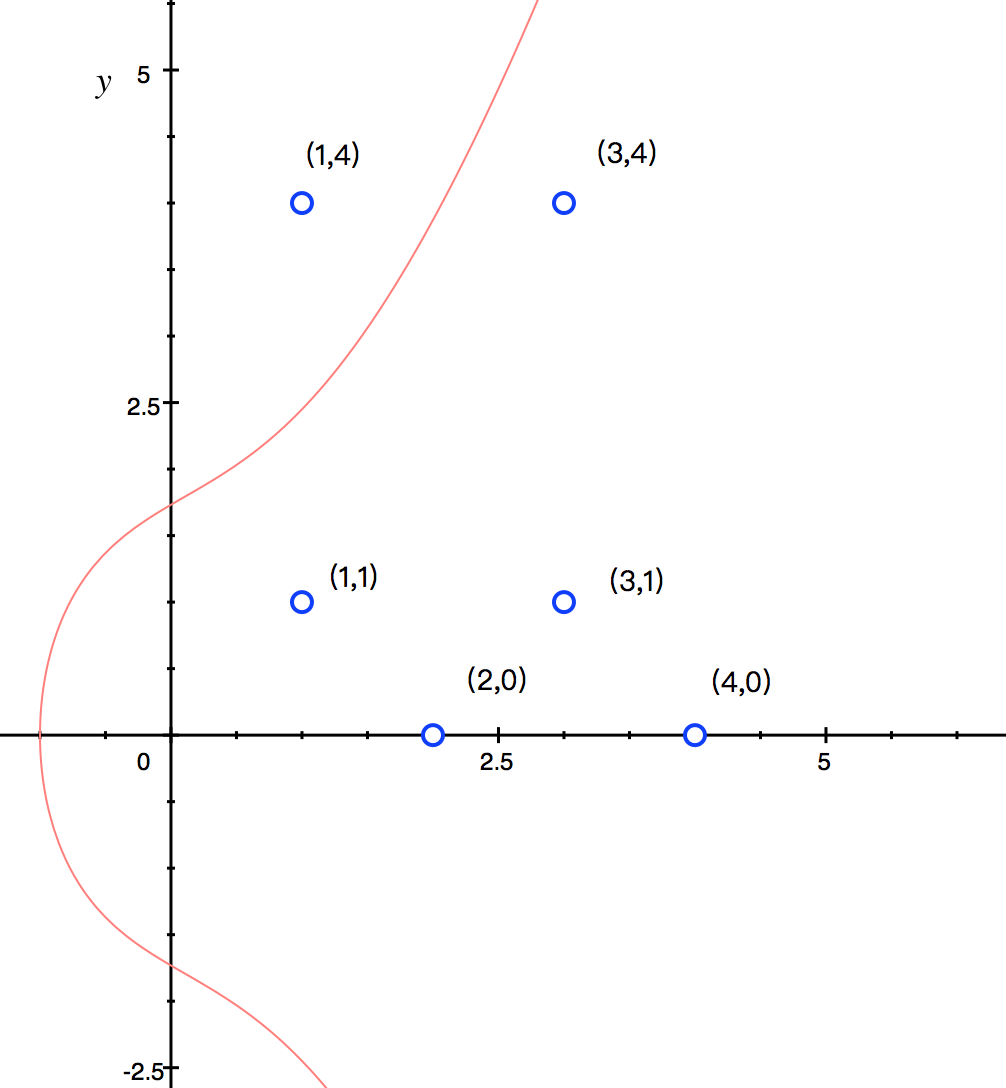
上述椭圆曲线共存在六个点$E={(1,1), (1,4), (2,0), (3,1), (3,4), (4,0)}$,根据前面的加法定义,可以举例计算一下:
$\mathcal{O}=(4,0)$,$\mathcal{O}+\mathcal{O}=\mathcal{O}$,满足定义1。
$P=(1,1),Q=(1,4)$,则$P+Q=\mathcal{O}$。注意到$4\equiv -1\bmod{5}$,符合定义3。
$P=(1,1),Q=(2,0)$,则$P+Q=(3,1)$。符合定义4。
$P=(1,1)$,则$P+P=2P=(3,4)$。符合定义5。
可以验证集合$E$以其加法操作构成一个群。
有限域$\mathcal{F}_p$上的标量乘法⌗
对于$\forall k \in Z, P\in E$,可以构造一个标量乘法$Q=kP,Q\in E$。根据前面的讨论,$E$为有限群,则$\exists n \in Z,nP=\mathcal{O}$,$n$称之为点$P$的阶。
以前面曲线$y^2 =x^3 +2x+3 \bmod{5}$为例子,选择$P=(1,1)$作为生成元,可以得到 $$1P=(1,1)$$ $$2P=(3,4)$$ $$3P=(2,0)$$ $$4P=(3,1)$$ $$5P=(1,4)$$ $$6P=(4,0)=\mathcal{O}$$ 故而,点$P$的阶为$6$。
椭圆曲线签名算法密码交换举例⌗
现在我们选定$(E,+,6,1,g=(1,1))$,假设通信双方为Alice和Bob:
Alice选择一个随机自然数$a=2$,然后将$g^{a}=2*g=(3,4)$发送给Bob
Bob选择一个随机自然数$b=3$,然后将$g^{b}=3*g=(2,0)$发送给Alice
Alice计算 $ (g^b )^{a}=2*(2,0)=(4,0)$
Bob计算 $ (g^a )^{b}=3*(3,4)=(4,0)$
此时,Alice和Bob可以共同协商出相同的结果$(4,0)$。
椭圆曲线数字签名算法(ECDSA)⌗
对于一个特定的椭圆曲线算法,假设其基点$G$的阶为$n$。 给定一个用户的密钥对$(d,D)$,小写字母为私钥,大写字母为公钥;待签名的信息为$M$,签名: $$Signature(M)=(r,s)$$
签名过程:
随机生成密钥对$(k, K)$,其中$K=(K_x, K_y)$
令$r = K_x \bmod n$,如果$r = 0$,则返回步骤1
计算$H = Hash(M)$,按照数据类型转换规则,将$H$转化为一个大端整数$e$
令$s = k^{-1} (e + rd) \bmod n$,若$s = 0$, 则返回步骤1
输出的$Signature(M)=(r,s)$即为签名。
验证过程:
计算$H = Hash(M)$,按照数据类型转换规则,将$H$转化为一个大端整数$e$
计算 $u_1 = s^{-1} e \bmod n$, $u_2 = s^{-1} r \bmod n$
计算 $K=(K_x, K_y) = u_1 G + u_2 D$, 如果 $K = \mathcal{O}$,则验证该签名无效
计算 $v = K_x \bmod n$,若$v = r$,则签名有效,否则签名无效。
secp256k1常量⌗
文献9中给出了secp256k1的常量具体值,这里给出椭圆曲线方程:
曲线方程 $y^2 =x^3 +7$
有限域$\mathcal{F}_p$的质数$p=2^{256} -2^{32} -2^9 -2^8 - 2^7 -2^6 - 2^4 -1$
椭圆曲线上的基点$(g_x,g_y)$ $$g_x=55066263022277343669578718895168534326250603453777594175500187360389116729240$$ $$g_y=32670510020758816978083085130507043184471273380659243275938904335757337482424$$
椭圆曲线上基点的阶为$115792089237316195423570985008687907852837564279074904382605163141518161494337$,cofactor为1。
参考文献⌗
- 浅说椭圆曲线
- An Elementary Proof of the Group Law for Elliptic Curves
- Lecture 10 - Elliptic Curve Cryptography, Wayne Patterson
- What is Elliptic Curve Cryptography
- An Introduction to the Theory of Elliptic Curves,Joseph H. Silverman
- The Arithmetic of Elliptic Curves, Joseph H. Silverman
- Guide to Elliptic Curve Cryptography,Darrel Hankerson,Alfred Menezes,Scott Vanstone
- SEC 1: Elliptic Curve Cryptography
- SEC 2: Recommended Elliptic Curve Domain Parameters